NHL EDGE: Skating Speed, Part 3

Impact on shot quantity and quality

Previously in this series, I examined what the NHL EDGE skating speed and distance data revealed about the difference between forwards and defensemen as well as the impact of role and fatigue. While I think my findings were interesting, the question remained did any of this really matter? In other words, does skating speed have a meaningful impact on whether teams win hockey games, or is it just trivia?

In this post, I demonstrate that skating speed does have a meaningful impact on shot quantity, though not on shot quality at even strength. However, an individual skater’s speed is less impactful. This post will wrap up the series for now, except for a small post covering miscellaneous topics that did not fit into any of the other pieces, though I plan to return to skating speed at some point in the future to dive into special teams.

Methodology

At a high level, I wanted to discover how average individual skating speed impacted shot quantity rates (corsi for and against per 60 minutes) and shot quality rates (xGoals for and against per 60 minutes) for each individual skater. Note that this exercise is meant to be purely descriptive, not predictive. That is, how much of previous results can we explain using skating speed.

However, this is not as simple as just looking at the speed of all the skaters on the ice and seeing how that correlates to corsi. I think the way to think of speed is as a micro stat or process stat; something that’s effect should be captured in the larger picture results. For example, if a larger player is able to use his size to his advantage to influence play, that should be baked into their overall shot share statistics, and including size as a variable should not provide any additional descriptive information.

To that end, I wanted to account for the ability of all the players on the ice to impact shot quantity and quality before seeing if skating speed provided any additional descriptive information. To do this, I used Evolving-Hockey’s xGAR model components. Specifically, I used even the strength rate for (RF) and rate against (RA) components when looking at shot quantity and quality for (QF) and quality against (QA) when looking at shot quality. Finally, I also wanted to make sure I was accounting for external factors. Score and venue effects are already well-known and I included additional terms for these.

To isolate speed as a factor, I ran total of sixteen of linear regressions looking at single game on-ice corsi for and against rates and xG for and against rates by position (forward and defensemen), both with and without variables for speed and analyzed the differences between including speed or not. The basic regression formula for shot quality used corsi for rate as the target variable and included predictors for score, venue, individual rate driving ability, forward teammate rate driving, defenseman teammate rate driving, opposing forward rate suppressing, and opposing defensemen rate suppressing. The full formula is included in the footnotes.¹ For shot quantity against rate, I used corsi against rate and reversed the rate driving and rate suppressing values for individuals, teammates, and opponents.

To account for skating speed, I included separate variables for each skater’s average speed at even strength in that game, the average speed of their forward teammates, the average speed of their defensive teammates, the average speed of their forward opponents, and the average speed of their defensive opponents.

Similarly, the regression for shot quality used Evolving-Hockey’s expected goals per 60 minutes as the target variable, with the same predictor variables, plus an additional variable to account for shot quality (corsi rate). This was intended to account for quality separate from quality.² The full formula is included in the footnotes.³ As with quantity, for quality against rate, quality driving and suppressing variables are reversed for individuals, teammates, and opponents.

Limitations and Assumptions

The most obvious limitation as that even with game-by-game data, the NHL EDGE data is presented in an aggregated format, rather than on a period, shift, or even second-by-second level. What this meant was that I aggregated the other predictors in each of my regressions. So, for example, instead of having a variable for score differential unique to each shift, I used an the average score difference for the entire game. That is, if a skater played twenty minutes in a game at even strength, and his team led by one for the last five minutes of the game that he was on the ice, his average score difference was 0.25 for the game.

Additional assumptions I made include:

• xGAR components are purely additive instead of containing interactions or diminishing/multiplicative impacts. This is almost certainly false, but it’s far outside the scope of the project to suss out chemistry effects between playing styles. Rather, my hope is that any more complex effects essentially cancel each other out in the aggregate.

• xGAR component impacts are discrete by position. Similar to the previous point, I doubt this is true, but hope that the effects cancel.

• xGAR components represent ability more closely than results. This is the goal of xGAR, according to my understanding, and during testing I found that the regressions performed better using xGAR components instead of regular GAR, which supports this assumption.

• NHL EDGE seems to treat empty net situations as even strength, as long as one team doesn’t have a power play, so I followed suit on this. Empty net situations are a small enough part of the game that in my testing this did not change the overall results dramatically.

• Skating speed has a linear impact. This may not be true at the furthest extremes, especially at the top end of skating speed, but in my testing there was not a notable improvement in results using a polynomial predictor versus a simple linear one, so I opted to use a linear predictor for easier interpretation.

Lastly, I did not perform any regressions on actual goals scored. This may seem odd considering that’s the most consequential metric for winning games, however, I did not think I was adequately able to capture finishing/saving impact with the data I had. xGAR does contain a shooting component, which I think would serve as a reasonable proxy for finishing talent, but I don’t think any of goalie WAR or GSAx or xSAA (my expected saves metric) captures goalie ability accurately. I hope to develop a measure of goaltender talent at some point, and I may return to this topic at that time, but for this article, I’m excluding actual goals from this analysis.

Results

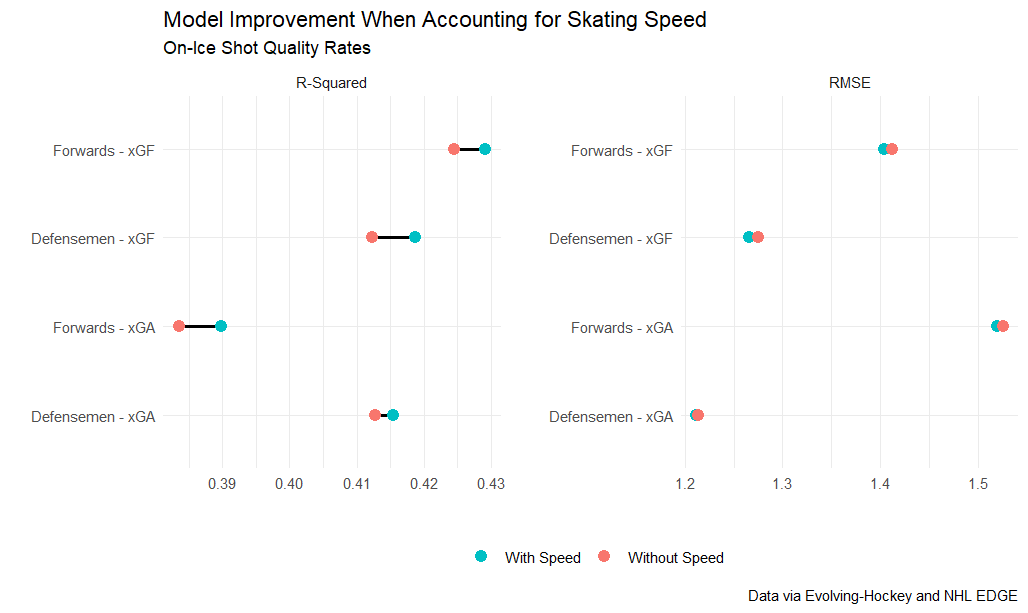
Including variables for speed improved the descriptive value of all the models examined, though the magnitude of the impact was greater for shot quantity than quality.

As the chart above shows, including predictive variables for speed increase the R-Squared value for every regression while also reducing the error. Interestingly, the largest improvement by far came in explaining single game corsi against rate for defensemen. In all, average skating speed explains over 4% of the game-to-game variation, which is quite a bit more than I expected at the start of the project. Across the rest of the regressions, speed explained roughly 2-2.5% of the game-to-game variation is shot quantity.

The impact on shot quality is muted, by comparison, though skating speed does still improve descriptive power.

Each model saw only a marginal improvement when accounting for skating speed. However, it is still noteworthy that skating speed improves the regressions, even after accounting for shot quality, which already includes the effect of skating speed. In other words, skating speed seems to have some explanatory power for both quantity and quality independent of each other.

Whose speed matters, and how does it matter?

So speed does add information beyond, just ability, situation, and QoT/QoC, but that raises the further questions of what impact each skating component had

To start with, I’ll look at the coefficients related to skating speed for each shot quality regression that included them. Almost every predictor was significant at 99.9% confidence, though the magnitude for each was fairly small.

There’s a lot to unpack here! The first thing I notice is that by position, the individual coefficients have the same sign (positive or negative) as the teammate coefficients for the same position. That is, individual forward’s average speed has a negative coefficient on corsi for rate, and so does their forward teammate’s average speed. Same goes for defensemen and corsi against rates. That consistency by position suggests to me that the signal is real and not random noise.

Similarly, with the exception of forward teammate’s average speed on corsi for rates, teammate and opponent impacts are the same sign across positions when the target variable is the same. Again, I interpret this to mean that this is a meaningful result.

Next, I notice that defensemen’s average speed has the largest coefficients generally, and opposing defensemen’s average speed in particular seems to have the greatest impact. I suspect this is picking up the impact of “activating” defensemen jumping into the rush as a fourth forward versus sitting back and playing more of a shutdown game.

Finally, there is a general trend that opponent’s skating faster being associated with lower shot quantity for and higher shot quantity against. For defensemen this trend is reversed: higher individual and speed and teammate speed increase shot quantity for and decrease it against. However, for forwards, increased individual and forward teammate speed tends to result in lower shot quantity both for and against. I had some difficulty interpreting this exception to the rule. My best guess is that faster skating forwards tend to be depth forwards, as discussed in part 2 of this series, and those forwards are tasked more often with playing a minimizing game rather than trying to score.

As mentioned previously, the impact of speed on shot quality is considerably smaller than on quantity. However, as with shot quantity, almost every predictor was statistically significant at 99.9% confidence.

Many of the same patterns listed above appear here as well. One extremely noteworthy exception is that opposing defensemen’s speed positively increases average shot quality for. Taken with my interpretation that increased opposing defensemen speed indicates activating, this suggests to me that activation does create higher quality chances going the other way. Furthermore, defensemen activating does not improve the average shot quality for (see also: individual defensemen and defensive teammate speed also have negative coefficients). Rather, the advantage of activating defensemen is entirely in extra volume generated and suppressed and results in giving up quality advantage.

Overall, increased skating speed seems to have a negative impact on shot quality, with the exception of defensemen activating increasing the shot quality against.

Future Work or Potential Areas of Improvement

There are still several areas of improvement. Most obvious to me is that average skating speed is still a very crude method of accounting for skating ability. I experimented a little bit with creating some kind of skating rating or separate ratings for hustle and acceleration using burst rates, top speed, and average speed, but the results were unsatisfactory to me.

Additionally, more can be done to account for expectations of role. It appears some of the forward results for both quantity and quality may be driven by expectations of role, where typically such a distinction doesn’t exist as strongly for defensemen.

Furthermore, this analysis excludes impact on actual goals. Repeating this analysis with expected goals weighted by shooter and goaltender talent may reveal a greater impact of skating speed on the final results of a game.

Lastly, just as a note of caution, this analysis assumes that the chain of causality is skating speed leading to shot quantity and quality results, but it is possible that this is not the case.

Conclusion

Skating speed generally has a strongly positive impact on shot quantity for and a suppressive effect on shot quantity against. Conversely, increased speed seems to reduce shot quality, both for and against. These effects are mostly consistent across positions, though the magnitude of the effect is greater for defensemen. Generally these impacts are small, but they are statistically significant, suggesting incorporating skating speed could improve existing models.

1

\(\begin{align*} \mathrm{CF/60}_t = \alpha &+ \beta_1\mathrm{Mean.Score.Differential}_t \\ &+ \beta_2\mathrm{Venue}_t \\ & + \beta_3\mathrm{Individual.RF}_t \\ & + \beta_4(\frac{1}{n}\sum_{k=1}^{n}\mathrm{Teammate.RF/60.Forwards}_k)_t \\ &+ \beta_5(\frac{1}{n}\sum_{k=1}^{n}\mathrm{Teammate.RF/60.Defensemen}_k)_t \\ &+ \beta_6(\frac{1}{n}\sum_{k=1}^{n}\mathrm{Opponent.RA/60.Forwards}_k)_t \\ &+\beta_7(\frac{1}{n}\sum_{k=1}^{n}\mathrm{Opponent.RA/60.Defensemen}_k)_t \\ &+ \epsilon \end{align*}\)

2. One thing I feel is can be improved in current hockey analytics discourse is the separation of quality from quantity. If a team has a 60% CF% in a game and a 60% xGF%, they didn’t really create more quality, they just created more chances of the same average quality and shouldn’t be treated as winning the shot quality battle.

\(\begin{align*} \mathrm{xGF/60}_t = \alpha &+ \beta_1\mathrm{Mean.Score.Differential}_t \\ &+ \beta_2\mathrm{Venue}_t \\ & + \beta_3\mathrm{Individual.QF}_t \\ & + \beta_4(\frac{1}{n}\sum_{k=1}^{n}\mathrm{Teammate.QF/60.Forwards}_k)_t \\ &+ \beta_5(\frac{1}{n}\sum_{k=1}^{n}\mathrm{Teammate.QF/60.Defensemen}_k)_t \\ &+ \beta_6(\frac{1}{n}\sum_{k=1}^{n}\mathrm{Opponent.QA/60.Forwards}_k)_t \\ &+\beta_7(\frac{1}{n}\sum_{k=1}^{n}\mathrm{Opponent.QA/60.Defensemen}_k)_t \\ & + \beta_8\mathrm{CF/60}_t \\ &+ \epsilon \end{align*}\)

3.